ФОРМИРОВАНИЕ ЭЛЕМЕНТАРНЫХ МАТЕМАТИЧЕСКИХ ПРЕДСТАВЛЕНИЙ У ДЕТЕЙ ДОШКОЛЬНОГО ВОЗРАСТА

ЖУРНАЛ Дошкольник.РФ

ФОРМИРОВАНИЕ ЭЛЕМЕНТАРНЫХ МАТЕМАТИЧЕСКИХ ПРЕДСТАВЛЕНИЙ У ДЕТЕЙ ДОШКОЛЬНОГО ВОЗРАСТА

Антонова Светлана Геннадьевна Воспитатель МБДОУ детский сад № 9 г. Павлово Нижегородская область

Арифметика является фундаментом, на котором строится способность правильно воспринимать действительность, и создаёт основу для развития ума и сообразительности в отношении практических вопросов. И. Песталоцци

Аннотация: в статье рассмотрена одна из актуальных проблем дошкольной педагогики – проблема формования элементарных математических представлений у детей дошкольного возраста, показано ее значение при формировании познавательных интересов и познавательных действий ребенка в различных видах деятельности.

Ключевые слова: формирование элементарных математических представлений у детей дошкольного возраста, математические развитие, цели и задачи ФЭМП.

На современном этапе развития образования, одним из ведущих принципов дошкольного образования является принцип развивающего обучения. Становление начальных математических знаний и умений стимулирует всестороннее развитие малышей, формирует абстрактное мышление и логику, совершенствует внимание, память и речь, что позволит ребёнку активно познавать и осваивать окружающий мир. Занимательное путешествие в страну геометрических фигур и арифметических задач станет прекрасным подспорьем в воспитании таких качеств, как любознательность, целеустремлённость и организованность.

Формирование элементарных математических представлений (ФЭМП), по определению А.В. Белошистой, – это целенаправленный и организованный процесс передачи и усвоения знаний, приемов и способов умственной деятельности детей дошкольного возраста в сфере математики [1, с. 14].

Результатом процесса ФЭМП является математическое развитие. Математическое развитие детей дошкольного возраста – это изменения в их познавательной деятельности, происходящие в результате формирования элементарных математических представлений и связанных с ними логических операций [1, с. 16].

Хотелось бы отметить, что данная область знания развивается не первое столетие. Так, в ΧVΙΙ – ΧΙΧ вв. вопросы содержания и методов обучения детей дошкольного возраста арифметике и формирования представлений о размерах, мерах измерения, времени и пространстве рассматривались в работах великих педагогов – Л. С. Выготским, Я.А. Коменского, И.Г. Песталоцци, К.Д. Ушинского, Л.Н. Толстым и др., в начале ХХ в. этими вопросами занимались Р.Л. Березина, З.А. Михайлова, Р.Л. Рихтерман, А.А. Столяр и др. Начиная со второй половины 1950-х г.г. вопросы формирования математических представлений детей дошкольного возраста рассматривались Р.Л. Березиной, В.В. Давыдовы, В.В. Даниловым, А.М. Леушиным, З.А. Михайловой, Р.Л. Непомнящей, Т.В. Тарунтаевой и другими [4]. Опираясь на труды Т. В. Тарантуевой, начальная математическая подготовка детей дошкольного возраста предусматривала обучение счету, развитие количественных представлений в пределах 1-го десятка, обучение решению и составлению элементарных арифметических задач. Кроме того, предполагает выполнение операций с множествами (наглядно представленными), проведение измерений при помощи условных мерок, а также развитие глазомера детей, формирование представлений о времени, о геометрических фигурах, формирование понимания пространственных отношений. Т.В. Тарунтаева отмечает, что в понятие «формирование математических представлений» входит такой объем материала, который значительно выходит за рамки развития у детей дошкольного возраста исключительно счетных навыков и умений, представляя собой, по сути, полноценную программу начального математического развития. Такая программа, по мнению педагога, должна обеспечить глубокое понимание детьми количественных и других отношений, а также заложить базу дальнейшего развития математического мышления у детей [7, с. 12].

По мнении, Л. С. Выготского, «наилучший возраст для обучения арифметике колеблется приблизительно между 6 и 8 годами» [3, с.336]. К.Д. Ушинский, в своих трудах, большое внимание удел вопросу развитии умственной деятельности. По его мнению: «Если рассудок есть особенная, прирожденная человеку способность, то она может одинаково работать, к чему бы ни была приложена, и развитие рассудка возможно одинаково на всяком предмете, который только упражняет его силу» [9, с.360]. Т. Д. Рихтерман, считал, что необходимо большое внимание уделять формированию у детей дошкольного возраста понятие время, как составляющей математических представлений. Он писал так: «Детям уже в дошкольном возрасте жизненно необходимо научиться самим ориентироваться во времени…… Умение регулировать и планировать деятельность во времени создает основу для развития таких качеств личности, как организованность, собранность, целенаправленность, точность, необходимых ребенку при обучении в школе и в повседневной жизни» [6, с. 3]. Проблемой развития памяти занимался и И. Г. Песталоцци: «Память, удерживающая ряды чисел, приковывает ум к их внутренним отношениям» [5, с. 72]. Этой же проблемой и условия успешного функционирования памяти занималась Г. А. Урунтаева, она пришла к следующим выводам: «Эффективность произвольной образной памяти напрямую зависит от степени трудности запоминания и воспроизведения признаков предмета, нарастающей в следующем порядке: цвет, форма, величина, количество, пространственное расположение объектов и их частей» [8, с. 6]. По ее мнению, умственное развитие является основополагающим направлением в формировании психики детей дошкольного возраста [8].

На сегодняшний день в образовании используется накопленный опыт педагогической науки, учитываются современные условия развития математического мышления ребенка и новые разработки современной педагогической науки в области математики. Развитие умения познавать предметы и явления, выделять свойства, выявлять зависимости и закономерности, сравнивать предметы по свойству – всё это позволяет формировать логические структуры мышления, которые являются фундаментом общего умственного и математического развития.

Термин «математика», как предмет изучения, отсутствует во ФГОС ДО. Задача формирования математических представлений является «проникающей» и имеет содержательные соответствия в различных образовательных областях, таких, например, как познавательное развитие.

В соответствии с ФГОС ДО, формирование элементарных математических представлений отнесено к образовательной области «Познавательное развитие». Данная область предполагает развитие интересов детей, становление их сознания; развитие воображения и творческой активности, а также формирование первичных представлений о себе, о других людях, об объектах окружающего мира, (форме, цвете, размере, материале, звучании, ритме, темпе, количестве, числе, части и целом, пространстве и времени, движении и покое, причинах и следствиях и др.) [10с, ст. 2. 6]. Одним из основных принципов дошкольного образования, в соответствии с ФГОС ДО, становится «формирование познавательных интересов и познавательных действий ребенка в различных видах деятельности» [10, ст. 1. 4, п.7].

Важнейшим итогом, по мнению А.В. Белошистой, предшкольной математической подготовки ребенка является не только накопление определенного запаса знаний и умений, сколько умственное развитие ребенка, формирование у него необходимых познавательных и умственных умений, которые являются базовыми для успешного усвоения в дальнейшем математического и любого другого обобщенного содержания[1]. Данная мысль соответствует требованиям ФГОС ДО, в котором ребенок должен обрести предпосылки учебной деятельности. Только после усвоения ребенком элементарных математических представлений его легче подготовить к усвоению более сложных математических задач на следующих ступенях развития.

Целью ФЭМП у детей дошкольного возраста являются: всестороннее развитие личности детей, осуществление их подготовки к школьному обучению, осуществление познавательного развития детей[1, с. 24].

При ФЭМП у детей дошкольного возраста ставятся следующие задачи:

формирование у детей системы элементарных математических представлений;
развитие элементарных основ математического мышления;
развитие у детей сенсорных процессов и способностей;
расширение, обогащение словаря и совершенствование связанной речи[2].

При выполнении работы по ФЭМП необходимо соблюдать следующие принципы: сознательности и активности, деятельностного подхода, научности и доступности, прочности, последовательности и систематичности, связи с жизнью, также соблюдаются принципы индивидуального и дифференцированного подходов и др. [2].

Процесс формирования элементарных математических представлений у детей дошкольного возраста включает в себя ряд разделов: «Количество и счет», «Величина», «Форма», «Ориентировка в пространстве», «Ориентировка во времени». Такое построение программы по формированию элементарных математических представлений остается постоянным во всех группах.

«Количество и счет», предполагает развитие представлений детей о числе, счете, множестве, об арифметических действиях, а также предполагает решение детьми элементарных текстовых задач.
«Величина» ориентирован на развитие представлений детей о величинах, о способах их сравнении и измерения (толщине, площади, длине, ширине, высоте, объеме, массе, времени).
«Форма» отражает развитие представлений детей о форме предметов, геометрических фигурах (плоских и объемных), их свойствах, а также существующих отношениях.
«Ориентировка во времени» содержит программный материал, направленный на развитие представлений детей о времени суток и их частях, о днях недели, месяцах и временах года, а также предполагает развитие у детей «чувства времени».
«Ориентировка в пространстве» предполагает, что дети учатся ориентироваться в отношении собственного тела, относительно себя самих, другого человека, расположенных вокруг предметов, а учатся ориентироваться в пространстве и на плоскости, в т.ч. на листе бумаги и в движении[2].

На сегодняшний день, наблюдается наличие большого количества общеобразовательных программ дошкольного образования, но каждая из них придерживается одного программного материала при формировании элементарных математических представлений у детей дошкольного возраста. программа второй младшей группы ориентирована на дочисловой период – на этом этапе дети учатся сравнивать предметы, знакомятся с их формой, учатся различать пространственные направления, а также ориентироваться во времени на элементарном уровне. В средней группе программа усложняется и наполняется новым содержанием, вводится счет при помощи числительных, изучают величину, форму предметов, учатся ориентироваться в пространстве и во времени. В старшей группе продолжается работа по обучению детей счету, закрепляются приобретенные умения и навыки, дети учатся сравнивать, измерять при помощи условной мерки (вводится деление предмета на равные части, развитие глазомера). Проводится работа по развитию представлений о геометрических фигурах, развитию умений ориентировки в пространстве и во времени. В подготовительной группе материал усложняется: предусматривается обязательное усвоение детьми материала, изучаемого в предыдущих группах, приобретенные знания, умения и навыки детей расширяются и углубляются. Это касается навыков счета, в т.ч. порядкового, вводится количественный состав числа из отдельных единиц и т.п., обратный счет, дети учатся составлять и решать простые арифметические задачи.

Подводя итог всему выше сказанному, хотелось отметить, что ФЭМП представляет собой целенаправленный и организованный процесс передачи и усвоения знаний, приемов и способов умственной деятельности детей дошкольного возраста в сфере математики. Результатом процесса формирования элементарных математических представлений является математическое развитие детей дошкольного возраста.

Список литературы

Белошистая, А.В. Теория и методика организации математического развития дошкольников / А.В. Белошистая. – Мурманск: МГПУ, 2010. – 256 с.
Веракса Н.Е. Основная общеобразовательная программа дошкольного образования «От рождения до школы»: Примерная общеобразовательная программа дошкольного образования. [Текст]/ Н.Е. Веракса, Т. С. Комарова, М. А. Васильев. – М.: Мозаика – Синтез, 2014. – 368с.
Выготский, Л. С. Педагогическая психология / Л.С. Выготский / Под. Ред. В.В. Давыдова. – М.: Педагогика-Пресс, 1996. – 536 с.
Габова, М.А. Средства математического развития ребенка: история и современность / М.А. Габова // Детский сад: теория и практика. – 2011. – № 3. – С.18-27.
Песталоцци, И. Г. Избранные педагогические сочинения: Т. 2. / под. Ред. В. А. Ротенберг, В. М. Кларина. – М.: Педагогика, 1981. – 416 с.
Рихтерман, Т. Д. Формирование представлений о времени у детей дошкольного возраста: Книга для воспитателя детского сада [Текст] / Т.Д. Рихтерман — 2-е изд. – М.: Просвещение, 1991. – 47с.
Тарунтаева, Т.В. Развитие элементарных математических представлений у дошкольников / Т.В. Тарунтаева. – М.: Просвещение, 2010. 64 с.
Урунтаева, Г. А., Афонькина Ю.А. Учимся запоминать/ Г. А. Урунтаева, Ю. А. Афонькина. – Мурманск: Научно-методический центр системы образования, 1993. – 93 с.
Ушинский, К. Д. Избранные педагогические сочинения.: Т. 1. / К. Д. Ушинский; под ред. А. И. Пискунова (отв. ред), [и др. ] – М.: «Педагогика», 1974. – 584с., Т.2 – С. 360.
ФГОС дошкольного образования//

Следующая >

Библиотека старых советских учебников по математике

Методика формирования элементарных математических представлений у дошкольников постоянно развивается, совершенствуется и обогащается результатами научных исследований и передового педагогического опыта.

В настоящее время благодаря усилиям ученых и практиков создана, успешно функционирует и совершенствуется научно обоснованная методическая система по формированию элементарных математических представлении у дошкольников. Еe основные элементы — цель, содержание, методы, средства и формы организации работы теснейшим образом связаны между собой и взаимообусловливают друг друга. Ведущим и определяющим среди них является цель, так как она социально детерминирована и носит объективный характер. Детский сад выполняет социальный заказ общества, подготавливая детей к изучению основ наук (в том числе и математики) в школе.

Советская педагогика и психология, опираясь на марксистско-ленинское учение, рассматривает развитие личности как процесс усвоения общественно-исторического опыта человечества. Этот опыт в его обобщенном виде передается молодому поколению взрослыми в процессе обучения. Ф. Энгельс писал, что индивидуальный опыт ребенка заменяется результатом опыта его предков. И усвоение детьми математических аксиом не что иное, как усвоение накопленной людьми наследственности.

Обучение и развитие находятся в диалектической связи. Опираясь на наличный уровень развития, обучение должно несколько опережать его. Это значит, что в процессе обучения необходимо ориентироваться не только на то, что способен делать сам ребенок, но и на то, что он может сделать при помощи взрослых, под их руководством, т. е. на перспективу, на зону ближайшего развития, в которой лежат обычно новые и более сложные действия и операции, чем те, которыми уже владеет ребенок. При их освоении используется «не только законченный уже на сегодняшний день процесс развития, не только уже завершенные его циклы, не только проделанные уже процессы созревания, но и те процессы, которые сейчас находятся в состоянии становления, которые только созревают, только развиваются»2. То, что ребенок недавно мог делать с помощью взрослого, через некоторое время в результате обучения выполняется им самостоятельно. «Зона ближайшего развития» становится «актуальным» уровнем развития.

Обучение ведет за собой развитие, являясь его источником и прокладывая ему пути. Каждый из этих взаимосвязанных процессов имеет свои закономерности. Неправомерно как отождествление, так и противопоставление их друг другу.

Однако до сих пор и в теории, и на практике не изжило себя полностью мнение, что, чем меньше возраст ребенка, тем меньше вмешательства должно быть в процесс его развития. Считается, что приобретение количественных, пространственных, временных представлений совершается само собой, стихийно в повседневной жизни и разнообразной деятельности детей. Существуют попытки жестко определять возрастные возможности в усвоении знаний, отрицать программность обучения маленьких детей. Так, швейцарский психолог Ж. Пиаже считает большой ошибкой думать о том, что ребенок воспринимает понятие числа и другие математические понятия непосредственно в обучении. По его мнению, эти понятия формируются у ребенка самостоятельно и спонтанно.

По мнению Ж. Пиаже, его учеников и последователей, овладение математическими понятиями происходит на основе логических операций классификации и сериации, которые ребенок открывает сам и обучиться которым практически невозможно. Они появляются довольно поздно, в 11—12 лет, т. е. уже в школьном возрасте. Такая точка зрения не решает проблемы математического развития и обучения детей в дошкольном возрасте.

Продуктивный подход к решению этой задачи сложился в советской педагогике и психологии на основе данных многочисленных исследований. Он заключается в следующем: в условиях рационально построенного обучения, учитывая возрастные возможности дошкольников, можно сформировать у них полноценные представлении об отдельных математических понятиях. Обучение при этом рассматривается как непременное условие развития, которое в свою очередь становится управляемым процессом, связанным с активным формированием элементарных математических представлений и логических операций. При таком подходе не игнорируется стихийный опыт и его влияние на развитие ребенка, но ведущая роль отводится целенаправленному обучению.

Под математическим развитием дошкольников следует понимать сдвиги и изменения в познавательной деятельности личности, которые происходят в результате формирования эле» ментарных математических представлений и связанных с ними логических операций.

Формирование элементарных математических представлений — это целенаправленный и организованный процесс передачи и усвоения знаний, приемов и способов умственной деятельности, предусмотренных программными требованиями. Основная его цель — не только подготовка к успешному овладению математикой в школе, но и всестороннее развитие детей.

§ 2. Методика формирования элементарных математических представлений и другие науки

Методика формирования элементарных математических представлений у детей в детском саду связана со многими науками, и прежде всего с темн, предметом изучения которых являются разные стороны личности и деятельности рсбенка-дошколышка, процесс его воспитания и обучения.

Наиболее тесная связь существует у нее с дошкольной педагогикой, наукой о коммунистическом воспитании детей. Методик?» формирования элементарных математических представлений опирается на разрабатываемые дошкольной педагогикой и дидактикой задачи обучения и умственного воспитания подрастающего поколения: принципы, условия, пути, содержание, средства, методы, формы организации и т. д. Связь эта по своему характеру взаимная: исследование и разработка проблем формирования элементарных математических представлений у детей в свою очерет» совершенствует педагогическую теорию, обогащая се новым фактическим материалом.

Многосторонние контакты существуют между частными методиками, изучающими конкретные закономерности процесса воспитания и обучения маленьких детей: методикой формирования элементарных математических представлений, развития речи, теорией и методикой физического воспитания и др.

Подготовка детей к усвоению математики в школе не может осуществляться успешно без связи с методикой начального обучения математике и теми аспектами самой математики, которые являются теоретической основой обучения дошкольников и младших школьников. Опора на эти науки позволяет, во-первых, определить объем и содержание знаний, которые должны быть освоены детьми в детском саду и служить фундаментом математического образования; во-вторых, использовать методы и средства обучения, в полной мере отвечающие возрастным особенностям дошкольников, требованиям принципа преемственности.

Реформой общеобразовательной и профессиональной школы поставлена задача повышения качества обучения всем общеобразовательным предметам, в том числе и математике. Общеизвестно, что при усвоении математических знаний у многих учащихся возникают серьезные затруднения, причиной которых, как правило, бывает недостаточная математическая подготовка в дошкольном возрасте.

Совершенствование содержания и методов обучения математике в школе предполагает новое отношение к подготовке детей в период, непосредственно предшествующий школьному обучению. В настоящее время уже внесены существенные изменения в программу развития математических представлении у дошкольников (увеличение объема устного счета, счет групп предметов, обучение измерению отдельных величин, расширение геометрических знаний и др.); найдены и апробированы более эффективные методы и средства обучения (моделирование, проблемные задачи и ситуации, развивающие и обучающие игры и т. д.). Связь с методикой обучения математике в начальной школе позволяет верно определить основные пути дальнейшего совершенствования методики формирования элементарных математических представлений у дошкольников.

Обучение должно строиться с учетом закономерностей развития познавательной деятельности, личности ребенка, что является предметом изучения психологических наук. Восприятие, представление, мышление, речь не только функционируют, но и интенсивно развиваются в процессе обучения.

Психологические особенности и закономерности восприятия ребенком множества предметов, числа, пространства, времени служат основой при разработке методики формирования элементарных математических представлений. Психология определяет возрастные возможности детей в усвоении знаний и навыков, которые не яв» лнются чем-то застывшим и меняются в зависимости от типа обучения. Современные психологические исследования показывают, что способности дошкольников в овладении математическими представлениями велики и до конца еще не раскрыты, полностью не изучены.

Рациональное построение процесса обучения связано с созданием оптимальных условий на основе анатомо-физиологических особенностей маленьких детей. Закономерности протекания физиологических процессов у дошкольников служат основой дли определения места и длительности занятий по формированию элементарных математических представлений для каждой возрастной группы детского сада, обусловливают саму их структуру, сочетание и чередование различных методов и средств обучения, разных по характеру видов деятельности (включение физкультминуток, дозирование учебно-познавательных задач и т. д.).

Методика формирования элементарных математических представлений относительно молодая научная педагогическая дисциплина, однако она имеет давние истоки. Исторический экскурс показывает, как постепенно изменялись концепции первоначального обучения математике в зависимости от запросов жизни и уровня развития самой математической науки, дает возможность критически оценить богатое наследие, избежать многих ошибок, учесть положительный опыт прошлого, а также результаты новейших исследований. В марксистско-ленинской теории она находит прочную методологическую основу, которая обеспечивает всестороннее и глубокое рассмотрение явления в его развитии, соблюдение принципа объективности, конкретности, единства теории и практики.

Связь с различными науками создает теоретическую базу методики формирования математических представлений у детей в детском саду.

§ 3. Исследование проблем формирования элементарных математических представлений у дошкольников

Долгое время концепции первоначального обучения маленьких детей числу и счету строились либо на основе умозрительных теоретических построений, либо путем эмпирического опыта. Выдающиеся мыслители прошлого (Я. А. Коменскин, И. Г. Песталоцци, К. Д. Ушннскнй, Л. Н. Толстой), видные деятели в области дошкольного воспитания за рубежом (Ф. Фребель, М. Монтессори) и в нашей стране (Е. И. Тихеева, Ф. Н. Блехер) успешно сочетали непосредственную работу с детьми с теоретическим осмыслением ее результатов.

Становление методики формирования математических представлений у дошкольников связано с применением экспериментальных методов исследования, которые стали внедряться в последнее время.

Научный поиск в этой области ведется в Институте дошкольного воспитания АПН СССР и в ряде других научных и учебных учреждений страны. В этой работе принимают участие и воспитатели, методисты, преподаватели.

В последние годы широкое развитие получили исследования проблем обучения шестилеток (АПН СССР, НИИ педагогических наук Украины, Грузии, Прибалтийских и других республик, Могилевский педагогический институт и др.). Эти исследования оказывают непосредственное влияние на теорию и практику формирования элементарных математических представлений у дошкольников.

В современных условиях в связи с переходом к обучению в школе детей с шестилетнего возраста особую значимость приобретает разработка методов совершенствования подготовки дошкольников к освоению школьной математики.

Исследования в области формирования элементарных математических представлений у детей непосредственно связаны с практикой и дают научные способы решения ее важнейших проблем. Разрабатываемые содержание» методические приемы, дидактические средства и формы организации работы находят применение в практике формирования элементарных математических представлений у детей в детском саду. Публикация основных результатов исследования делает их достоянием широких кругов дошкольных работников. Рекомендации ученых учитываются при переработке программы развития элементарных математических представлений в детском саду. Периодически в ней производятся изменения, вносятся новые требования и задачи с учетом результатов научных исследований. Выводы и рекомендации ученых способствуют совершенствованию работы детских садов но развитию математических представлений у детей, служат основой для последующих научных исследований.

Студенческие, учебно- и научно-исследовательские работы (контрольные, курсовые, выпускные, дипломные), в которых приобретаются знания, навыки и умения, необходимые будущему специалисту, должны отвечать требованиям актуальности, новизны, теоретической и практической значимости, объективности и достоверности, как и любые другие научные работы, посвященные проблемам математического развития дошкольников.

«Формирование математических представлений у детей дошкольного возраста»

автор: Чумак Анастасия Валерьевна

воспитатель МБДОУ «Русскополянский детский сад №5»

«Формирование математических представлений у детей дошкольного возраста»

«Формирование математических представлений у детей дошкольного возраста»

Актуальность проекта.

Взрослые не перестают удивляться, как много может усвоить, запомнить ребёнок в первые годы. Период дошкольного детства относительно всей жизни человека недолго, а как он насыщен познанием! Каждый день приносит ребёнку что-то новое, неизведанное; становится близким и понятным ранее недоступное.

Велик поток информации, который обрушивает на маленького человека окружающая жизнь. Источником познания дошкольника является чувственный опыт. Диапазон его зависит от того, насколько тонко ребёнок владеет суммой специальных действий (рассматривание, ощупывание, сравнение, сопоставление, выделение главного и второстепенного и т.д.), влияющих на восприятие и мышление.

Обучению дошкольников началам математики в настоящее время отводится важное место. Это вызвано целым рядом причин: началом школьного обучения с шести лет, обилием информации, получаемой ребенком, повышением внимания к компьютеризации, желанием сделать процесс обучения более интенсивным, стремлением родителей в связи с этим, как можно раньше научить ребенка узнавать цифры, считать, решать задачи.

Преследуется главная цель: вырастить детей людьми, умеющими думать, хорошо ориентироваться во всем, что их окружает, правильно оценивать различные ситуации, с которыми они сталкиваются в жизни, принимать самостоятельные решения. Взрослые зачастую спешат дать ребенку набор готовых знаний, суждений, которые он впитывает как губка. Однако всегда ли это дает ожидаемый результат? Скажем, надо ли заставлять ребенка заниматься математикой, если ему это скучно?

Практика дошкольного образования показывает, что на успешность обучения влияет не только содержание предлагаемого материала, но также форма его подачи, которая способна вызвать заинтересованность ребенка и его познавательную активность.

Занимательность может быть задана необычайной формой обучения. Надо только найти золотую середину: не усложнять — дети не поймут и не упрощать, облегчая учение, — дети будут постоянно искать легкие пути, чтобы поменьше трудиться. Получая пищу для своего ума, ребенок охотно участвует в занятиях, ждет их, радуется им.

Занимательный материал не только увлекает ребенка, но и способствует совершенствованию наблюдательности, внимания, памяти, мышления и речи дошкольника. Стихотворный материал, загадки, считалки применяются в зависимости от целей познавательного общения. Возможности их использования широки: на групповых занятиях в детском саду, при индивидуальной работе с детьми в семье, на викторинах, досугах, праздниках, в ходе познавательной беседы, в игротеке, когда дети принимают родителей в гости и играют с ними в математические игры.

Занимательная математика ставит дошкольников в условия поиска, пробуждает интерес к победе, следовательно, дети стремятся быть быстрыми, находчивыми.

Проблема, решаемая при реализации проекта.

В старшей группе воспитывается 23 воспитанника: 12 мальчиков и 11 девочек.

На занятиях по формированию элементарных математических представлений у многих детей старшей группы направленности отсутствовал интерес к математике, существовали затруднения с мышлением, вниманием.

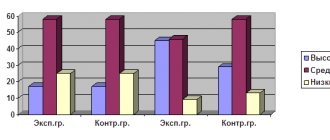
В начале года данная область была реализована на 1,5 балла

, что составило в итоге
37, 5 %
— низкий показатель по группе.

Чтобы повысить уровень математического развития, активность детей, развить у них интерес к математике, решили использовать занимательный материал: загадки, стихи, дидактические игры, занимательные вопросы, задачи-шутки, математические сказки, пословицы и поговорки, пальчиковую гимнастику, лабиринты, логические концовки, математические КВНы.

Контингент участников проекта:

воспитанники старшей группы; воспитатель; родители воспитанников.

Цель проекта:

Формирование элементарных математических представлений у детей старшего дошкольного возраста через занимательный материал.

Задачи:

Развивать интерес к математике у детей старшего дошкольного возраста, эмоциональную отзывчивость через игры с математическим содержанием.
Формирование базисных математических представлений, речевых умений.
Способствовать развитию мыслительных операций (анализ, синтез, сравнение, классификация), логического мышления.
Развивать самостоятельность познания, поощрять проявления творческой инициативы, находчивости.
Увеличить объём внимания и памяти.
Развивать речь, умение высказывать и обосновывать свои суждения;
Воспитывать интерес к предмету и процессу обучения в целом.

Содержание проекта.

I этап –

подготовительный.

Заинтересовать родителей в реализации проекта.

Сообщение: «Образовательные и воспитательные задачи по формированию элементарных математических представлений в старшей группе» на родительском собрании.

Индивидуальные беседы о результатах диагностики.

Создание условий для реализации проекта.

Подбор занимательного материала для проведения индивидуальных и фронтальных занятий с детьми, изготовление игрового математического материала.

Первичная диагностика.
Изучение методической литературы по теме.

Поиск материалов в Интернете.

II этап –

основной.

Реализация основных видов деятельности по направлениям проекта.

Презентация проекта – открытое занятие по формированию элементарных математических представлений для родителей.

III этап –

итоговый.

Проведение итоговой диагностики.

Сбор и обработка методических и практических материалов.
Соотнесение прогнозируемых результатов с полученными.

Обобщение материалов проекта.

Ожидаемые результаты.

положительная динамика мониторинга по формированию элементарных математических представлений у детей старшего дошкольного возраста;
формирование операций логического мышления (анализ, синтез, сравнение, классификация, обобщение);
применение детьми математических знаний и умений в самостоятельной деятельности, проявлений творческой инициативы;
осознание родителями важности формирования элементарных математических представлений у детей с помощью занимательного материала, расширение знаний родителей о занимательном материале;
развитие у детей интереса к математике, стремления к преодолению трудностей.

Реализация проекта.

Развитию внимания и сообразительности способствуют задачи-шутки, головоломки, предостерегающие ребёнка от поспешных и необоснованных выводов. Их не следует решать, как обычные задачи, используя то или иное арифметическое действие. Эти задачи должны побуждать детей рассуждать, мыслить, находить ответ, используя имеющиеся уже знания.

Использование задач-шуток и задач на сообразительность поможет разнообразить и оживить занятия с детьми. Кроме этого, задачи подобного рода можно использовать при проведении математических досугов, весёлых встреч дошкольных знатоков, КВНов.

Занимательный материал не только развлекает детей, даёт возможность им отдохнуть, переключиться, но и заставляет их задуматься, развивает самостоятельность, инициативу, направляет на поиски нетрадиционных способов решения, стимулирует развитие нестандартного мышления.

Детям даётся возможность внимательно выслушать загадку, запомнить её содержание, отгадать. Загадка загадывается эмоционально, неторопливо.

Дети знают много считалок и чаще всего с их помощью выбирают ведущего в играх. Этот же приём можно использовать и на занятиях по математике. Чтобы поднять активность детей на занятии, нужно не назначать детей, а делать это с помощью считалки.

Для формирования полноценных математических представлений и для развития познавательного интереса у дошкольников очень важно наряду с другими методами использовать занимательные проблемные ситуации. Жанр сказки позволяет соединить в себе и то и другое. Сам сюжет, сказочные персонажи привлекают детей. Вживаясь в события сказки, ребёнок как бы становится её действующим лицом. При этом повышается познавательная активность: он стремится вмешаться в ситуации и повлиять на них. Живой интерес, который возникает у ребёнка, можно использовать для повышения эффективности обучения.

Материалы для занятий с детьми.

Дид. игра «Покажи столько же»
Игра с палочками.
«Собери фигуру из частей »
«Четвертый лишний»
Игра «Белый лист».
Игра «Зашиваем ковёр»
«Найди соседа»
«Дни недели»
«Сосчитай и сравни количество»
Игра «Круг, треугольник, квадрат»
Задачи-шутки, головоломки, лабиринты, задания на сообразительность.
Считалки, загадки.
«Логические раскраски»
«Модель года»
. «Формы и объекты»

Математические сказки.

«Необыкновенные приключения в городе математических загадок».
«В гостях у гнома-часовщика, или история о том, как не опоздать в школу».
«Как Топ учился математике».
«Женькины игры».
«Помоги Незнайке найти дорогу».
«Догадайся сам!».
«Как Нина учила брата».

Полученные результаты.

Положительная динамика роста математического развития детей.

В начале года данная область была реализована на 1,5 балла, что составило в итоге 37, 5 % — низкий показатель по группе; на конец года – 2, 3 балла (57,4 % средний показатель).

Дети проявляют познавательную активность, творческую инициативу, стараются преодолевать трудности в совместной с воспитателем и самостоятельной деятельности.
Повышение педагогической грамотности и заинтересованности родителей в формировании элементарных математических представлений у детей.
Оформлен уголок занимательной математики.
Проведено итоговое занятие «Математическое королевство» для родителей.

Литература.

Ерфеева Т.И. и др. Математика для дошкольников: Кн. Для воспитателя дет. сада/Т.И. Ерофеева, Л.Н. Павлова, В.П. Новикова. – М.: Просвещение, 1992. – 191 с.: ил.
Математика от трёх до семи: Учебно-методическое пособие для воспитателей детских садов/ Авт. – сост. З.А. Михайлова, Э.Н. Иоффе; Худ. И.Н. Ржевцева. – СПБ.: «Акцидент», 1997. – 176 с.: Ил.
Нищева Н.В. ИГРАЙКА. Игры и упражнения для формирования и развития элементарных математических представлений и речи у дошкольников.- СПб.: «ДЕТСТВО-ПРЕСС», 2003. – 16 с., ил.
Петерсон Л.Г.,. Кочемасова Е.Е. Игралочка. Практический курс математики для дошкольников. Методические рекомендации. – «Баласс», 1998. – 160 с.
Помораева И.А, Позина В.А. Формирование элементарных математических представлений. – Москва: Издательство Мозайка-Синтез, 2015. – 60с.
Тихомирова Л.Ф. Развитие познавательных способностей детей. Популярное пособие для родителей и педагогов. – Ярославль: Академия развития, 1996. – 192 с., ил.
nsportal.ru/…/ispolzovanie-zanimatelnoy-matematike-v-individualnoy-ra…
www.maam.ru/…/konspekt-nod-s-detmi-starsh
ei-grupy-po-fyemp-itogov…

«Формирование математических представлений у детей дошкольного возраста»

Задачи математического развития дошкольников.

Осваиваемое содержание должно соответствовать возрастным и индивидуальным возможностям дошкольников, быть ориентированным на зону их ближайшего развития.

6. Взаимосвязь понятий «развитие», «обучение», «воспитание». Математические способности.

Математическое развитие детей дошкольного возраста осуществляется как в результате приобретения ребенком знаний в повседневной жизни (прежде всего, в результате общения со взрослым), так и путем целенаправленного обучения на занятиях по формированию элементарных математических знаний.

Именно элементарные математические знания и умения детей следует рассматривать как главное средство математического развития.

В процессе обучения у детей развивается способность точнее и полнее воспринимать окружающий мир, выделять признаки предметов и явлений, раскрывать их связи, замечать свойства, интерпретировать наблюдаемое; формируются мыслительные действия, приемы умственной деятельности, создаются внутренние условия для перехода к новым формам памяти, мышления и воображения.

Психологические экспериментальные исследования и педагогический опыт свидетельствуют о том, что благодаря систематическому обучению дошкольников математике у них формируются сенсорные, перцептивные, мыслительные, вербальные, мнемические и другие компоненты общих и специальных способностей.

Задатки индивида превращаются в конкретные способности посредством учения.

Разница в уровнях развития детей, как показывает опыт, выражается главным образом в том, какими темпами и с какими успехами они овладевают знаниями.

Однако при всем важном значении обучения в психическом развитии личности последнее нельзя сводить к учению. Развитие не исчерпывается теми изменениями личности, которые являются прямым следствием обучения. Оно характеризуется теми «умственными поворотами», которые происходят в голове ребенка, когда он научается говорить, читать, считать, усваивает социальный опыт, передаваемый ему взрослым.

Как показывают исследования (А. В. Запорожец, Д. Б. Эльконин, В. В. Давыдов и др.), развитие идет дальше того, что усваивается в тот или иной момент обучения. В процессе и под влиянием обучения происходит целостное, прогрессирующее изменение личности, ее взглядов, чувств, способностей. Благодаря обучению расширяются возможности дальнейшего усвоения нового, более сложного материала, создаются новые резервы обучения.

Между обучением и развитием существует взаимная связь. Обучение активно содействует развитию ребенка, но и само опирается на его уровень развития. В этом процессе многое зависит от того, насколько обучение нацелено на развитие.

Обучение может по-разному развивать ребенка в зависимости от его содержания и методов. Именно содержание и его структура являются гарантами математического развития ребенка.

Под способностями понимается комплекс индивидуально — психологических особенностей человека, отвечающих требованиям данной деятельности и являющиеся условием успешного выполнения. Таким образом, способности — сложное, интегральное, психическое образование, своеобразный синтез свойств, или, как их называют компонентов.

Общий закон образования способностей состоит в том, что они формируются в процессе овладения и выполнения тех видов деятельности, для которых они необходимы.

Способностине есть нечто раз и навсегда предопределённое, они формируются и развиваются в процессе обучения, в процессе упражнения, овладения соответствующей деятельностью, поэтому нужно формировать, развивать, воспитывать, совершенствовать способности детей и нельзя заранее точно предвидеть как далеко может пойти это развитие.

Говоря о математических способностях как особенностях умственной деятельности, следует прежде всего указать на несколько распространенных среди педагогов заблуждений.

Во-первых, многие считают, что математические способности заключаются прежде всего в способности к быстрому и точному вычислению (в частности в уме). На самом деле вычислительные способности далеко не всегда связаны с формированием подлинно математических (творческих) способностей.

Во-вторых, многие думают, что способные к математике школьники отличаются хорошей памятью на формулы, цифры, числа. Однако, как указывает академик А. Н. Колмогоров, успех в математике меньше всего основан на способности быстро и прочно запоминать большое количество фактов, цифр, формул.

Наконец, считают, что одним из показателей математических способностей является быстрота мыслительных процессов. Особенно быстрый темп работы, сам по себе, не имеет отношения к математических способностям. Ребенок может работать медленно и неторопливо, но, в то же время вдумчиво, творчески, успешно продвигаясь в усвоении математики.

Крутецкий В.А. в книге «Психология математических способностей дошкольников» различает девять способностей (компонентов математических способностей):

1) Способность к формализации математического материала, к отделению формы от содержания, абстрагированию от конкретных количественных отношений и пространственных форм и оперированию формальными структурами, структурами отношений и связей;

2) Способность обобщать математический материал, вычленять главное, отвлекаясь от несущественного, видеть общее во внешне различном;

3) Способность к оперированию числовой и знаковой символикой;

4) Способность к «последовательному, правильно расчленённому логическому рассуждению», связанному с потребностью в доказательствах, обосновании, выводах;

5) Способность сокращать процесс рассуждения, мыслить свернутыми структурами;

6) Способность к обратимости мыслительного процесса (к переходу с прямого на обратный ход мысли);

7) Гибкость мышления, способность к переключению от одной умственной операции к другой, свобода от сковывающего влияния шаблонов и трафаретов;

Математическая память. Можно предположить, что её характерные особенности также вытекают из особенностей математической науки, что это память на обобщения, формализованные структуры, логические схемы;

9) Способность к пространственным представлениям, которая прямым образом связана с наличием такой отрасли математики как геометрия.

⇐ Предыдущая2Следующая ⇒

Рекомендуемые страницы: